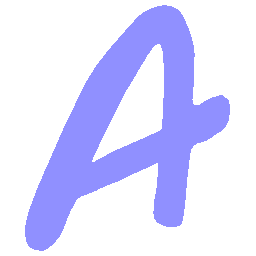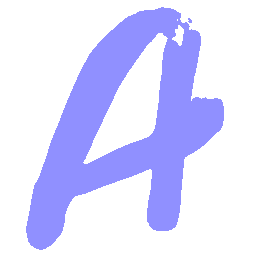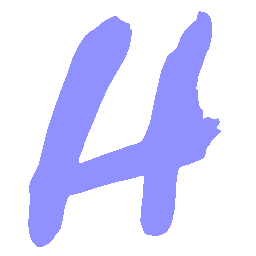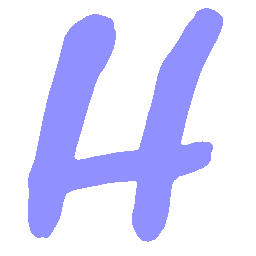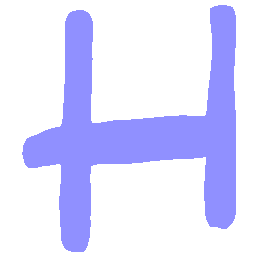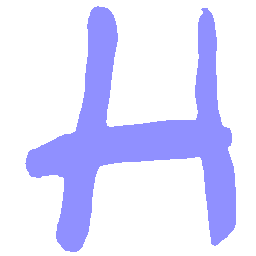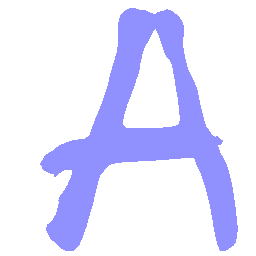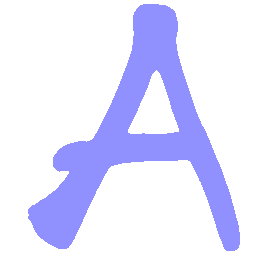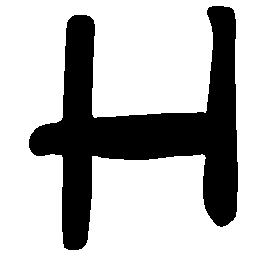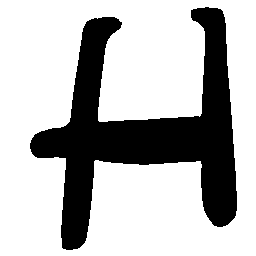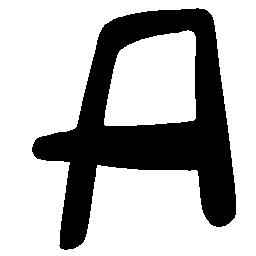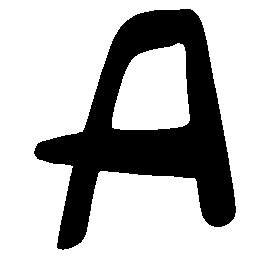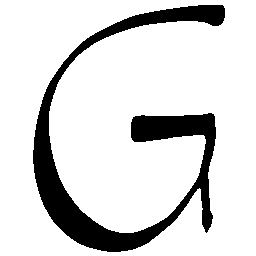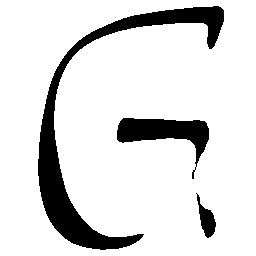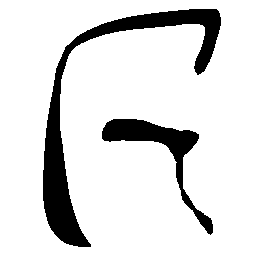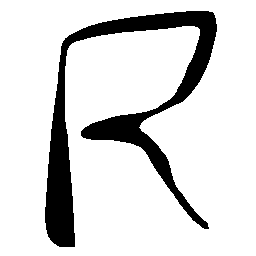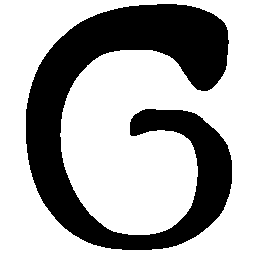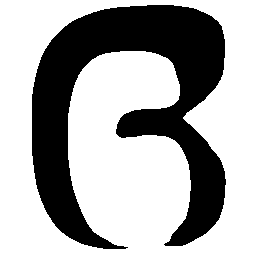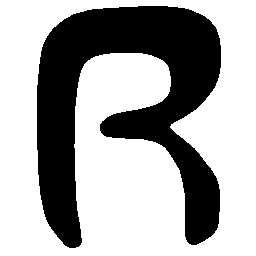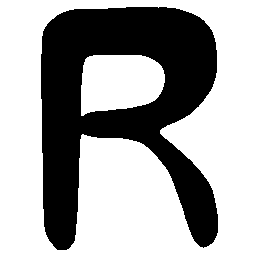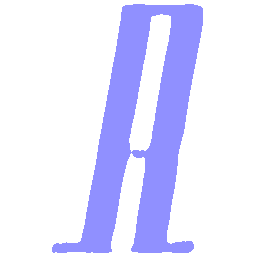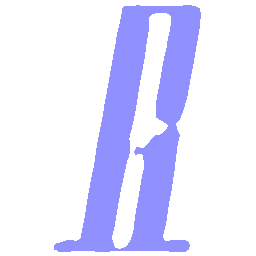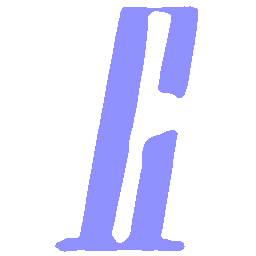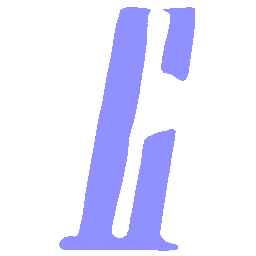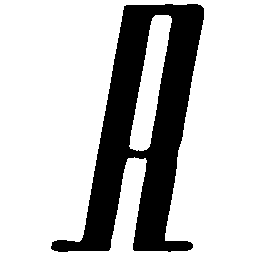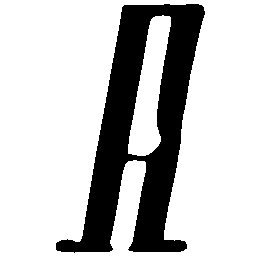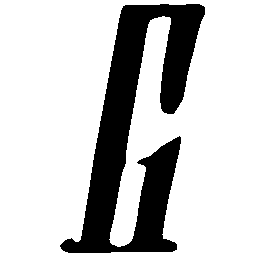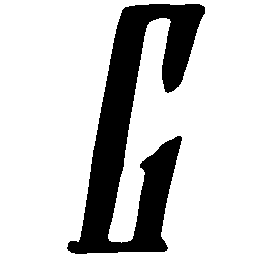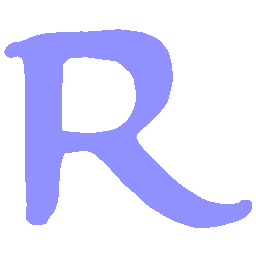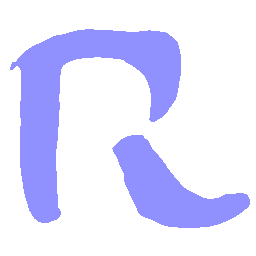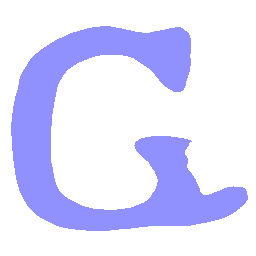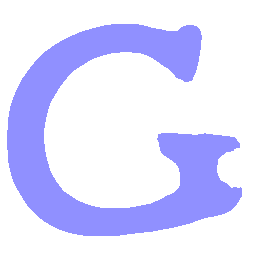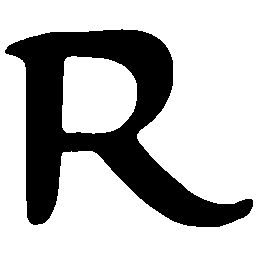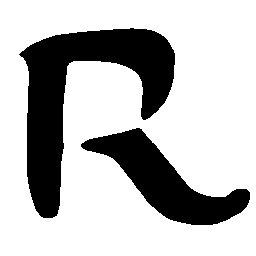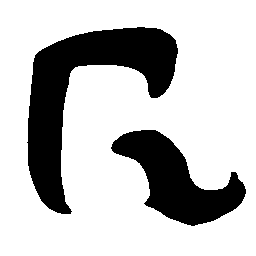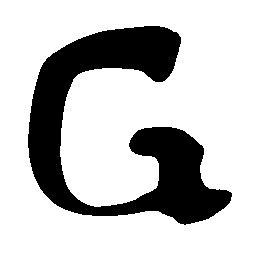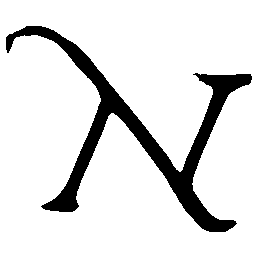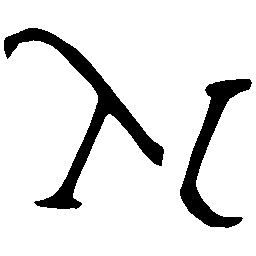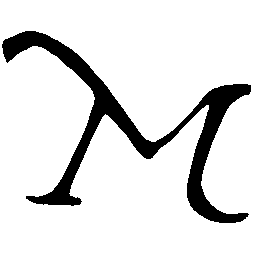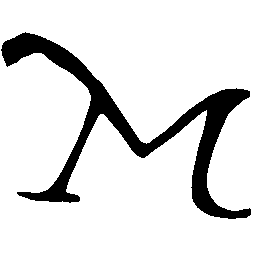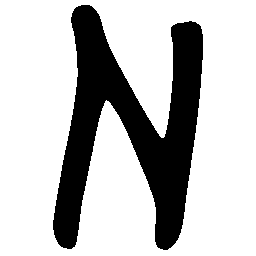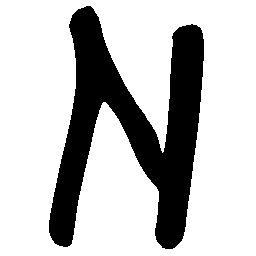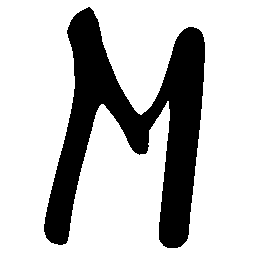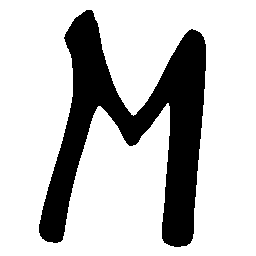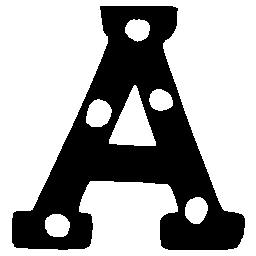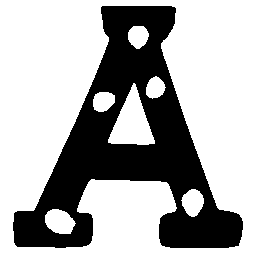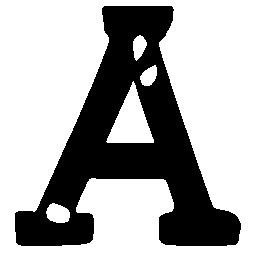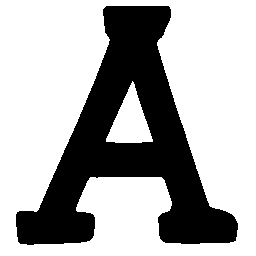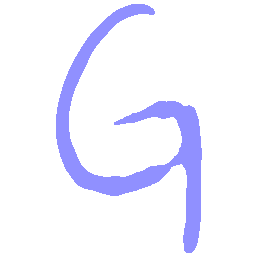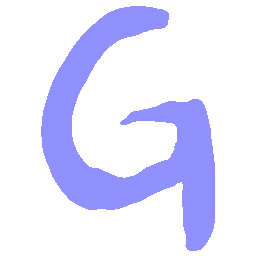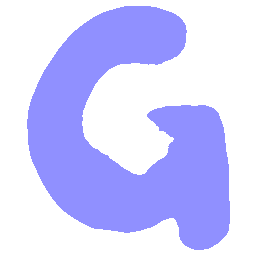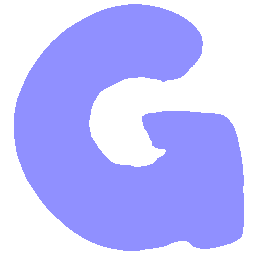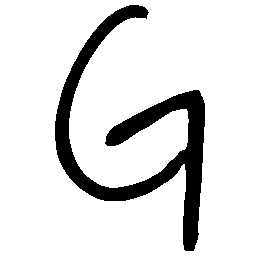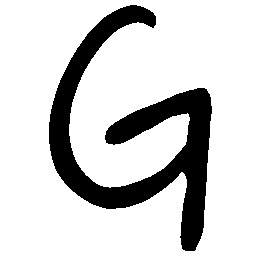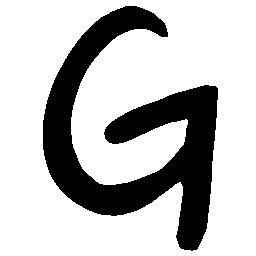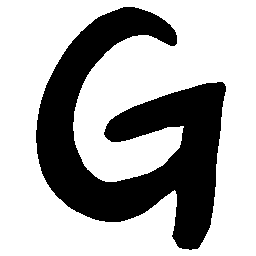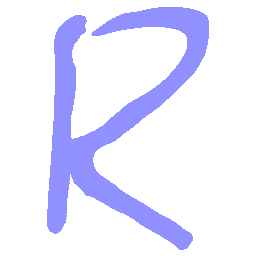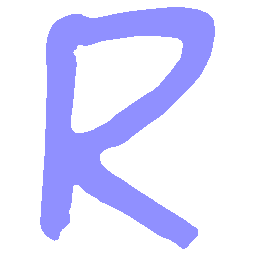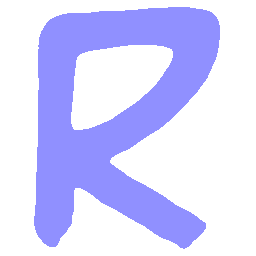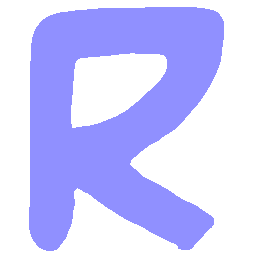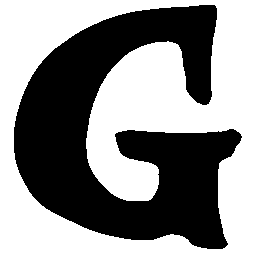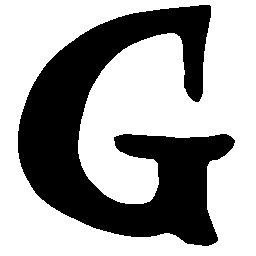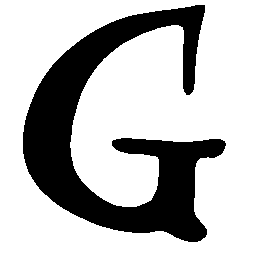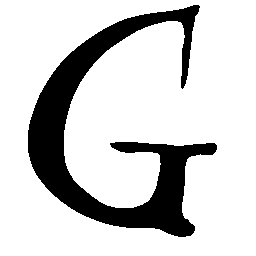UNIST: Unpaired Neural Implicit Shape Translation Network
UNIST is able to learn both style-preserving content alteration(a-d) and content-preserving style transfer(e-i) between two unpaired domains of shapes.
- Abstract -
We introduce UNIST, the first deep neural implicit model for general-purpose, unpaired shape-to-shape translation, in both 2D and 3D domains. Our model is built on autoencoding implicit fields, rather than point clouds which represents the state of the art. Furthermore, our translation network is trained to perform the task over a latent grid representation which combines the merits of both latent-space processing and position awareness, to not only enable drastic shape transforms but also well preserve spatial features and fine local details for natural shape translations. With the same network architecture and only dictated by the input domain pairs, our model can learn both style-preserving content alteration and content-preserving style transfer. We demonstrate the generality and quality of the translation results, and compare them to well-known baselines.
- Video -
- Method -
Overview of our framework for unpaired neural implicit shape-to-shape translation, which consists of two separately trained networks. The autoencoding network (top) learns to encode and decode binary voxel occupancies for shapes from both the source and target domains, where the encoder maps an input shape to a latent grid representation \(\mathcal{Z}\). In the 2D case, the latent feature at any query point \(p\) is obtained via bilinear interpolation over the latent codes stored in \(\mathcal{Z}\). The translation network (bottom) employs the pre-trained autoencoder network above to transform the translation problem into a latent space. In that space, a generator learns to: (1) translate source-domain codes \(\mathcal{Z}_{\chi_{1}}\) into target-domain codes \(\mathcal{Z}_{\chi_{1\rightarrow 2}}\). (2) preserve target-domain codes, from \(\mathcal{Z}_{\chi_{2}}\) to \(\mathcal{Z}_{\chi_{2\rightarrow 2}}\). \(\mathcal{Z}_{\chi_{1\rightarrow 2}}\) is passed to the pre-trained implicit decoder to obtain the final target shape resulting from the generator network.
- Results -
Latent Grid Interpolation (regular encoding vs. position-aware encoding)
UNIST with regular encoding generates compact translated shapes during interpolation as per
inherent nature of implicit representation.
UNIST with position-aware encoding further preserves
spatial features and fine local details for natural and well-behaved translations.
\(M \rightarrow N \)
\(N \rightarrow M \)
\(Solid \rightarrow Dotted \)
\(Dotted \rightarrow Solid \)
\(Regular \rightarrow Italic \)
\(Italic \rightarrow Regular \)
\(Regular \rightarrow Bold \)
\(Bold \rightarrow Regular \)
\(Sharp \rightarrow Smooth \)
\(Smooth \rightarrow Sharp \)
UNIST with regular encoding generates compact translated
shapes during interpolation as per inherent nature of implicit representation.
UNIST with position-aware encoding further preserves
spatial features and fine local details for natural and well-behaved translations.
\(Chair \rightarrow Table \)
\(Table \rightarrow Chair \)
\(w \, Armrest \rightarrow w/o \, Armrest \)
\(w/o \, Armrest \rightarrow w \, Armrest \)
\(Tall \rightarrow Short \)
\(Short \rightarrow Tall \)
2D Comparison
UNIST is capable of producing shapes with significantly better visual quality as it reproduces small stylistic features as well as preserves topological features.
3D Comparison
UNIST produces more compact translated shapes with better preservation of spatial features and details in both mesh and point cloud representations.
- Citation -
@inproceedings{chen2022unist,
title={UNIST: Unpaired Neural Implicit Shape Translation Network},
author={Chen, Qimin and Merz, Johannes and Sanghi, Aditya and Shayani, Hooman and Mahdavi-Amiri, Ali and Zhang, Hao},
booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
year={2022}
}